Normality has been shown to help provide more stable machine learning models and improve the accuracy of these models in the long term.
The problem is everyone is using their power transformer wrong.
This 2-minute guide will show you how to correctly use the yeo-johnson power transformer, why you’d use it over the box-cox transformation, and some general advice on improving your models.
Let’s jump right in
How do you use power transformation in Python?
# imports
import pandas as pd
import numpy as np
import random
# as always, a public dataset
# https://www.kaggle.com/datasets/mattiuzc/stock-exchange-data
df = pd.read_csv('stock-data.csv')
# for this, we're going to use the
# open minus close to predict tomorrows close price
df = df[['Open Minus Close','Tomorrows Close']].dropna()
# lets take every 10th line, since the dataset is massive
df = df.iloc[::10,:]
# see our columns
df.head()

# import our powertransformer
from sklearn.preprocessing import PowerTransformer
from sklearn.model_selection import train_test_split
# define it
pt = PowerTransformer()
## ******* Remember to split before you apply your transformer ************
X = df[['Open Minus Close']].values
y = df[['Tomorrows Close']].values
## stock data is time series
## we turn off shuffle here
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.20,\
random_state=32,
shuffle=False)
## now we apply our transformer and get the lamdbas
# from only our train set
yeo_X_train = pt.fit_transform(X_train)
# we can see the difference
pd.DataFrame(X_train).hist(bins=60)
pd.DataFrame(yeo_X_train).hist(bins=60)
Before (Not Exactly Zero Centered, Wide Range of Values

After (Zero Centered, More Even On Both Sides)
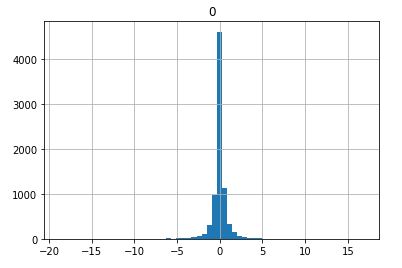
We also notice our data is standardized
What is a Johnson transformation?
The Johnson transformation is a statistical tool to help guide data distributions towards normality.
This can be useful when working with data that has a skewed distribution, as the transformed data will be easier to work with and interpret.
Who created the Yeo-Johnson Transformation?
The Yeo-Johnson Transformation was created by Yeo and Johnson. In December 2000, In-Kwon Yeo and Richard A. Johnson released a journal article titled “A New Family of Power Transformations to Improve Normality or Symmetry.”
Within this article, they introduced a new idea: The Yeo-Johnson Transformation
You can find the original article here
Why do we transform data in Python?
Depending on your data type, you might want to embed or transform your data before feeding it into your machine learning algorithm.
For one, you can often create better models by transforming your data.
This is because certain transformations can help stabilize your data, removing things like skew and making it more accurate.
Also, by transforming your data, you can sometimes improve the performance of your algorithms since we can take care of things like heteroskedasticity and the robust effects of outliers.
** Be sure to read at the bottom about taking care of outliers **

Advantages of The Yeo-Johnson Transformation over Box-cox?
The advantage of the Yeo-Johnson transformation over the box-cox transformation is that, by default, the input (or parameter) of the Yeo-Johnson transformation can be a negative value.
This is a huge advantage over the box-cox transformation since we don’t have to generate strictly positive values before applying the transformation.
When Should You Not Use A Power Transformation?
You should not use a power transformation as a crutch. If your variable has outliers, these need to be identified before you apply the yeo-johnson transform.
Many believe forcing outliers into their distribution’s fringes is okay since it will loosely resemble a normal distribution.

This has dramatic consequences, as outlier points have huge effects on your output’s mean and standard deviation.
Do you use power transformation before or after splitting your data?
You should always perform a power transform on your training set after splitting your data.
Since we have to act like our test set doesn’t exist yet, we’ll need to derive our lambdas from just the training set and apply them to the test set.
This is a common mistake in many data pipelines, applying transformations to the whole dataset and splitting.
This is known as data leakage, where we’ve accidentally leaked some insights from our test data (which we’re not supposed to know exists) into our training set.
These tactics can be useful when working with data that has a skewed distribution, as the transformed data will be easier to work with and interpret.

